1. 5.4 识别直积

本段是第 5.4 节的引言，它概述了本节即将探讨的核心主题。让我们逐句来理解。

第一句：“到目前为止，我们已经看到直积可以用来从“较小”的群构造“较大”的群，也可以将有限生成 Abel 群分解为循环因子。”

• 从“较小”的群构造“较大”的群：这指的是外直积 (External Direct Product) 的概念。如果我们有两个群 $H$ 和 $K$，我们可以构造一个新的群 $H \times K$，这个新群的元素是形如 $(h, k)$ 的有序对，其中 $h \in H$，$k \in K$。新群的阶数是 $|H| \times |K|$，通常比 $H$ 和 $K$ 都大。这是一种“合成”或“建造”新群的方法。
• 将有限生成 Abel 群分解为循环因子：这指的是有限生成阿贝尔群基本定理。该定理说明，任何一个有限生成的阿贝尔群都可以被唯一地（在同构意义下）分解成若干个循环群的直积。例如，一个复杂的阿贝尔群 $G$ 可能同构于 $Z_{p_1^{a_1}} \times Z_{p_2^{a_2}} \times \dots \times Z_{p_k^{a_k}}$。这是一种“分解”或“分析”现有群结构的方法，类似于将一个正整数分解为素数乘积。

第二句：“甚至某些非 Abel 群，即使以其他形式给出，也可以分解为较小群的直积。”

• 这句话扩展了直积的应用范围。直积不仅仅适用于阿贝尔群（元素可交换的群），也可能适用于非阿贝尔群。一个非阿贝尔群 $G$ 有可能被发现与两个或多个更小的群（其中至少一个是非阿贝尔群）的直积 $H \times K$ 是同构的。这意味着 $G$ 的结构在本质上等同于 $H$ 和 $K$ 两个群结构的“并排”组合。

第三句：“本节的目的是指出一个判据，以识别何时一个群是其某些子群的直积，并用一些例子说明该判据。”

• 这句话点明了本节的核心任务。前面提到的“分解”群，引出了一个关键问题：给定一个群 $G$，我们如何判断它能否被看作是其内部某些子群 $H$ 和 $K$ 的直积？这种情况下，我们讨论的是内直积 (Internal Direct Product)。
• 判据 (Criterion)：本节将提供一个或一组明确的条件。如果我们有一个群 $G$ 和它的一些子群，只要这些子群满足了这些条件，我们就可以断定 $G$（或者 $G$ 的某个子群）同构于这些子群的直积。
• 例子：通过具体的群（如二面体群 $D_{2n}$、对称群 $S_n$ 等）作为例子，来展示这个判据如何实际应用。

在正式给出识别直积的定理之前，文本引入了一个重要的辅助工具：换位子 (commutator)。换位子是衡量群中元素交换程度的标尺。

第一句：“在此之前，我们先介绍一些关于换位子的标准记号和基本结果，这将简化表述，并将在第6章考虑幂零群时再次使用。”

• 这句话说明引入换位子的动机。首先，它是简化后续定理表述的语言工具。其次，它是一个非常基础且重要的概念，在后续更高级的群论主题（如幂零群和可解群）中会反复出现。

定义部分

(1) 元素之间的换位子

• 原文：“定义 $[x, y]=x^{-1} y^{-1} x y$，称为 $x$ 和 $y$ 的换位子。”
• 解释：对于群 $G$ 中的任意两个元素 $x$ 和 $y$，它们的换位子被定义为一个特定的乘积组合：$[x, y] = x^{-1} y^{-1} x y$。
• 核心思想：这个表达式有什么特殊之处？让我们来看一下：
• 如果 $x$ 和 $y$ 是可交换的，即 $xy = yx$。
• 那么我们可以推导：$x^{-1}y^{-1}xy = x^{-1}(y^{-1}y)x = x^{-1}(e)x = x^{-1}x = e$（其中 $e$ 是单位元）。
• 反过来，如果 $[x, y] = e$，即 $x^{-1}y^{-1}xy = e$。
• 两边左乘 $yx$，得到 $(yx)(x^{-1}y^{-1}xy) = (yx)e$，即 $y(xx^{-1})y^{-1}xy = yx$，简化为 $yey^{-1}xy = yx$，即 $yy^{-1}xy = yx$，最终得到 $xy = yx$。
• 结论：$[x, y] = e$ 当且仅当 $x$ 和 $y$ 可交换。
• 因此，换位子 $[x, y]$ 的值“偏离”单位元 $e$ 的程度，就反映了 $x$ 和 $y$ “不可交换”的程度。如果一个群是阿贝尔群，那么其中任意两个元素的换位子都是单位元 $e$。

(2) 子集之间的换位子子群

• 原文：“定义 $[A, B]=\langle[a, b] \mid a \in A, b \in B\rangle$，由来自 $A$ 和 $B$ 的元素的换位子生成的群。”
• 解释：这扩展了换位子的概念，从单个元素对扩展到两个子集 $A$ 和 $B$。
• 步骤：

1. 首先，我们考虑所有可能的元素对 $(a, b)$，其中 $a$ 来自子集 $A$，$b$ 来自子集 $B$。
2. 对每一对 $(a, b)$，我们计算它们的换位子 $[a, b] = a^{-1}b^{-1}ab$。
3. 我们就得到了一个换位子的集合：$S = \{[a, b] \mid a \in A, b \in B\}$。
4. $[A, B]$ 被定义为由这个集合 $S$ 中所有元素生成的子群。
   • 生成子群 ($\langle \dots \rangle$)：由一个集合 $S$ 生成的子群，是包含 $S$ 的最小的子群。它的元素是 $S$ 中元素及其逆元的任意有限乘积。例如，$s_1, s_2 \in S$，那么 $s_1s_2$，$s_1^{-1}$，$s_2s_1s_2^{-1}$ 等都在 $\langle S \rangle$ 中。仅仅是换位子本身的集合不一定构成一个群（比如两个换位子的乘积不一定是另一个换位子），所以需要“生成”操作来确保闭合性，从而形成一个合法的子群。

(3) 群的换位子子群

• 原文：“定义 $G^{\prime}=\langle[x, y] \mid x, y \in G\rangle$，由 $G$ 的元素的换位子生成的 $G$ 的子群，称为 $G$ 的换位子子群。”
• 解释：这是第 (2) 部分的一个特例，其中子集 $A$ 和 $B$ 都取为整个群 $G$。
• $G'$（也记作 $[G, G]$）是由群 $G$ 中所有可能的换位子 $[x, y]$（其中 $x, y \in G$）生成的子群。
• $G'$ 包含了衡量群 $G$ “整体非交换性”的全部信息。如果 $G'$ 是一个平凡子群（即 $G'=\{e\}$），那么 $G$ 中所有元素都相互交换，所以 $G$ 是一个阿贝尔群。反之，如果 $G$ 是阿贝尔群，显然 $G'=\{e\}$。
• $G'$ 本身是一个非常重要的子群，我们将在下一段命题中看到它的许多关键性质。它有时也被称为导群 (derived subgroup)。

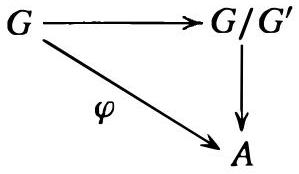
本段提出了一个包含五个重要性质的命题，深刻揭示了换位子及换位子子群在群论中的核心地位。

引言部分

• 原文：“$x$ 和 $y$ 的换位子是 1 当且仅当 $x$ 和 $y$ 可交换，这解释了术语。以下命题展示了换位子如何度量 $G$ 中 $x y$ 和 $y x$ 之间的“差异”。”
• 解释：再次强调了换位子的核心作用：它是衡量可交换性的标尺。“1” 在这里是乘法群中单位元的通用写法，有时也写为 $e$。换位子这个术语的来源就是因为它与 "commute"（交换）有关。接下来的命题将从不同角度深化这个思想。

命题 7 详解

(1) 换位子是 $xy$ 和 $yx$ 的“桥梁”

• 原文：“$x y=y x[x, y]$（特别地，$x y=y x$ 当且仅当 $[x, y]=1$）。”
• 逐步解释：这个等式给出了 $xy$ 和 $yx$ 的精确关系。
• 从换位子的定义 $[x, y] = x^{-1}y^{-1}xy$ 出发。
• 我们想从这个定义中解出 $xy$。
• 在等式两边同时左乘 $yx$：

$yx[x, y] = yx(x^{-1}y^{-1}xy)$

• 运用结合律：$yx[x, y] = y(xx^{-1})y^{-1}xy = y(e)y^{-1}xy = (yy^{-1})xy = exy = xy$。
• 于是，我们证明了 $xy = yx[x, y]$。
• 意义：这个式子表明，$xy$ 可以看作是先交换顺序变成 $yx$，然后再“补偿”一个换位子 $[x, y]$。这个换位子就是两者之间的“差异”或“修正因子”。
• 特别地：如果 $xy=yx$，那么 $yx = yx[x,y]$，两边消去 $yx$，得到 $[x, y] = 1$。反之，如果 $[x, y]=1$，那么 $xy = yx \cdot 1 = yx$。这再次确认了换位子与可交换性的等价关系。

(2) 正规子群的换位子判据

• 原文：“$H \unlhd G$ 当且仅当 $[H, G] \leq H$。”
• 逐步解释：这是一个极其有用的判断一个子群是否为正规子群的充要条件。
• 回顾正规子群定义：$H$ 是 $G$ 的正规子群（$H \unlhd G$），当且仅当对于任意 $g \in G$ 和任意 $h \in H$，都有 $g^{-1}hg \in H$。这个 $g^{-1}hg$ 称为 $h$ 的共轭。
• 证明 $H \unlhd G \implies [H, G] \leq H$：
• 假设 $H \unlhd G$。我们要证明 $[H, G] \leq H$。
• $[H, G]$ 是由形如 $[h, g]$（$h \in H, g \in G$）的元素生成的子群。我们只需证明所有这些生成元都在 $H$ 中。
• 考虑一个生成元 $[h, g] = h^{-1}g^{-1}hg$。
• 因为 $H \unlhd G$，所以 $g^{-1}hg \in H$。
• 因为 $H$ 是一个子群，它对乘法和求逆封闭。既然 $h \in H$，那么 $h^{-1} \in H$。
• $H$ 中有两个元素：$h^{-1}$ 和 $(g^{-1}hg)$。它们的乘积也必须在 $H$ 中。
• 因此，$h^{-1}(g^{-1}hg) = [h, g]$ 属于 $H$。
• 所有生成元都在 $H$ 中，所以它们生成的子群 $[H, G]$ 也包含在 $H$ 中，即 $[H, G] \leq H$。
• 证明 $[H, G] \leq H \implies H \unlhd G$：
• 假设 $[H, G] \leq H$。我们要证明 $H \unlhd G$。
• 这意味着对于任意 $h \in H, g \in G$，换位子 $[h, g] = h^{-1}g^{-1}hg$ 属于 $H$。
• 我们需要证明 $g^{-1}hg \in H$。
• 从 $[h, g] \in H$ 出发，两边左乘 $h$，得到 $h(h^{-1}g^{-1}hg) \in H$（因为 $h \in H$ 且 $H$ 是子群）。
• 计算得 $g^{-1}hg \in H$。
• 这正是正规子群的定义，所以 $H \unlhd G$。
• 意义：这个判据将正规性（一个关于共轭运算不变性的几何概念）转化为了一个关于换位子子群的代数包含关系，非常简洁和强大。

(3) 换位子子群的特殊性质

• 原文：“对于 $G$ 的任何自同构 $\sigma$，$\sigma[x, y]=[\sigma(x), \sigma(y)]$，$G^{\prime}$ char $G$，且 $G / G^{\prime}$ 是Abel 群。”
• 逐步解释：这一条包含三个结论。
• 结论一：自同构保持换位子结构 $\sigma[x, y]=[\sigma(x), \sigma(y)]$
• 自同构 ($\sigma \in \text{Aut}(G)$) 是一个从群 $G$ 到自身的同构映射，即保持群运算的 bijective 函数：$\sigma(ab) = \sigma(a)\sigma(b)$。
• 证明：

$\sigma([x, y]) = \sigma(x^{-1}y^{-1}xy)$

因为 $\sigma$ 是同态，所以 $\sigma(a^{-1}) = (\sigma(a))^{-1}$。

$= \sigma(x^{-1})\sigma(y^{-1})\sigma(x)\sigma(y)$

$= (\sigma(x))^{-1}(\sigma(y))^{-1}\sigma(x)\sigma(y)$

根据换位子的定义，这正是 $[\sigma(x), \sigma(y)]$。

• 结论二：换位子子群是特征子群 $G^{\prime} \text{ char } G$
• 特征子群 (Characteristic Subgroup) 定义：一个子群 $K \leq G$ 是特征子群，如果对于 $G$ 的任何自同构 $\sigma$，都有 $\sigma(K) = K$。即 $K$ 在所有自同构下保持不变。
• 证明：$G'$ 是由所有换位子 $[x, y]$ 生成的。
• 对任意一个生成元 $[x, y] \in G'$，我们刚证明了 $\sigma([x, y]) = [\sigma(x), \sigma(y)]$。由于 $\sigma$ 是满射，$\sigma(x)$ 和 $\sigma(y)$ 可以取遍 $G$ 中所有元素，所以 $[\sigma(x), \sigma(y)]$ 也是 $G'$ 的一个生成元。
• 这意味着 $\sigma$ 把 $G'$ 的生成集映射到了自身。因此，由这些生成元构成的整个子群也被映射到自身，即 $\sigma(G') = G'$。
• 所以 $G'$ 是 $G$ 的一个特征子群。
• 重要推论：特征子群一定是正规子群。因为共轭运算 $i_g(x) = gxg^{-1}$ 是一种特殊的自同构（内自同构），所以特征子群在所有共轭下不变，满足正规子群的条件。因此 $G' \unlhd G$。
• 结论三：商群 $G/G'$ 是阿贝尔群
• 商群 $G/G'$ 的元素是 $G'$ 的陪集，形如 $xG'$。运算是 $(xG')(yG') = (xy)G'$。
• 证明：我们要证明对于任意两个陪集 $xG'$ 和 $yG'$，它们是可交换的，即 $(xG')(yG') = (yG')(xG')$。
• $(xG')(yG') = (xy)G'$
• $(yG')(xG') = (yx)G'$
• 我们需要证明 $(xy)G' = (yx)G'$。根据陪集的性质，这等价于 $(yx)^{-1}(xy) \in G'$。
• $(yx)^{-1}(xy) = x^{-1}y^{-1}xy = [x, y]$。
• 根据 $G'$ 的定义，任何换位子 $[x, y]$ 都在 $G'$ 中。
• 因此 $(xy)G' = (yx)G'$ 成立。$G/G'$ 是阿贝尔群。
• 意义：$G/G'$ 被称为 $G$ 的阿贝尔化 (abelianization)。它是在“杀死”$G$ 中所有非交换性（通过将所有换位子视为单位元）后得到的“最接近”$G$ 的阿贝尔群。

(4) $G/G'$ 是“最大”的阿贝尔商群

• 原文：“$G / G^{\prime}$ 是 $G$ 的最大Abel 商群，其意义在于，如果 $H \unlhd G$ 且 $G / H$ 是Abel 群，则 $G^{\prime} \leq H$。反之，如果 $G^{\prime} \leq H$，则 $H \unlhd G$ 且 $G / H$ 是Abel 群。”
• 逐步解释：这揭示了 $G'$ 的一个普适性质 (universal property)。
• 证明 $G/H$ 是阿贝尔群 $\implies G' \leq H$：
• 假设 $H \unlhd G$ 且 $G/H$ 是阿贝尔群。
• 这意味着对于任意 $x, y \in G$，在商群 $G/H$ 中有 $(xH)(yH) = (yH)(xH)$。
• 即 $(xy)H = (yx)H$。
• 这等价于 $(yx)^{-1}(xy) \in H$。
• $(yx)^{-1}(xy) = x^{-1}y^{-1}xy = [x, y]$。
• 所以，对于任意 $x, y \in G$，都有 $[x, y] \in H$。
• 这意味着所有换位子都在 $H$ 中。而 $G'$ 是由所有换位子生成的最小子群，因此 $G'$ 必然被包含在 $H$ 中，即 $G' \leq H$。
• 证明 $G' \leq H \implies H \unlhd G$ 且 $G/H$ 是阿贝尔群：
• 假设 $G' \leq H$。
• 证明 $H \unlhd G$：我们知道 $G'$ char $G$，所以 $G' \unlhd G$。根据格同构定理（第三同构定理的应用），$G$ 中包含 $G'$ 的子群 $H$ 与 $G/G'$ 中的子群 $H/G'$ 一一对应。由于 $G/G'$ 是阿贝尔群，它的所有子群都是正规的，所以 $H/G' \unlhd G/G'$。这对应回 $G$ 中就是 $H \unlhd G$。
• 证明 $G/H$ 是阿贝尔群：根据第三同构定理，$G/H \cong (G/G') / (H/G')$。一个阿贝尔群 ($G/G'$) 的商群（$(G/G')/(H/G')$）必然是阿贝尔群。因此 $G/H$ 是阿贝尔群。
• 意义：“最大”的意义在于，任何一个能产生阿贝尔商群的正规子群 $H$，都必须“吞掉”整个换位子子群 $G'$。$G'$ 是所有这类正规子群中最小的一个。因此，对应的商群 $G/G'$ 就是“最大”的那个，因为分母最小。

(5) 同态的分解性质

• 原文：“如果 $\varphi: G \rightarrow A$ 是从 $G$ 到Abel 群 $A$ 的任何同态，则 $\varphi$ 通过 $G^{\prime}$ 分解，即 $G^{\prime} \leq \operatorname{ker} \varphi$ 且以下图可交换”
• 逐步解释：这是性质 (4) 的同态语言版本，也是一个非常重要的普适性质。
• 同态 $\varphi: G \rightarrow A$，其中 $A$ 是阿贝尔群。
• 考虑 $G$ 中任意一个换位子 $[x, y]$。我们看看它被 $\varphi$ 映射到哪里：

$\varphi([x, y]) = \varphi(x^{-1}y^{-1}xy)$

$= \varphi(x^{-1})\varphi(y^{-1})\varphi(x)\varphi(y)$

$= (\varphi(x))^{-1}(\varphi(y))^{-1}\varphi(x)\varphi(y)$

$= [\varphi(x), \varphi(y)]$。

• 因为 $\varphi(x)$ 和 $\varphi(y)$ 都是阿贝尔群 $A$ 中的元素，所以它们是可交换的。
• 因此，它们在 $A$ 中的换位子 $[\varphi(x), \varphi(y)]$ 是 $A$ 的单位元 $e_A$。
• 这意味着 $\varphi([x, y]) = e_A$。
• 这对 $G$ 中所有的换位子都成立。所以，所有的换位子都在 $\varphi$ 的核 ($\operatorname{ker} \varphi$) 中。
• 由于 $G'$ 是由所有换位子生成的，并且核是一个子群，所以整个 $G'$ 都被包含在核里面，即 $G' \leq \operatorname{ker} \varphi$。
• 交换图的意义：
• 图中有三个群 $G, G/G', A$ 和三个映射 $\pi, \varphi, \bar{\varphi}$。
• $\pi: G \rightarrow G/G'$ 是自然投射，$g \mapsto gG'$。
• $\varphi: G \rightarrow A$ 是给定的同态。
• 因为 $G' \leq \operatorname{ker} \varphi$，根据同态基本定理的推论，存在一个唯一的同态 $\bar{\varphi}: G/G' \rightarrow A$ 使得 $\varphi = \bar{\varphi} \circ \pi$。
• 这就是“$\varphi$ 通过 $G'$ 分解”的精确含义。任何到阿贝尔群的同态，都可以被看作是先进行“阿贝尔化”（$G \rightarrow G/G'$），然后再从这个阿贝尔化的群映出。

本段给出了命题7中五个性质的详细证明过程。

证明 (1)

• 原文：“这直接源自 $[x, y]$ 的定义。”
• 解释：如前一节的分析，从定义 $[x, y] = x^{-1}y^{-1}xy$ 出发，在等式两边左乘 $yx$，利用结合律和逆元的性质 $a a^{-1}=e$，即可直接推导出 $xy = yx[x, y]$。这是一个直接的代数变形，故原文一笔带过。

证明 (2)

• 原文：“根据定义，$H \unlhd G$ 当且仅当对于所有 $g \in G$ 和所有 $h \in H$，$g^{-1} h g \in H$。对于 $h \in H$， $g^{-1} h g \in H$ 当且仅当 $h^{-1} g^{-1} h g \in H$，因此 $H \unlhd G$ 当且仅当对于所有 $h \in H$ 和所有 $g \in G$，$[h, g] \in H$。因此 $H \unlhd G$ 当且仅当 $[H, G] \leq H$，这正是 (2)。”
• 解释：这是一个非常精炼的逻辑链条。

1. 第一步 (定义)：$H \unlhd G \iff \forall g \in G, \forall h \in H, g^{-1}hg \in H$。这是正规子群的定义。
2. 第二步 (等价变形)：因为 $H$ 是一个子群，它对逆元和乘法封闭。所以，如果 $h \in H$，那么 $h^{-1} \in H$。
   • 如果 $g^{-1}hg \in H$，那么 $h^{-1} \cdot (g^{-1}hg)$ 也一定在 $H$ 中。这个乘积就是 $[h, g]$。
   • 反过来，如果 $[h, g] = h^{-1}g^{-1}hg \in H$，那么 $h \cdot (h^{-1}g^{-1}hg)$ 也一定在 $H$ 中。这个乘积就是 $g^{-1}hg$。
   • 所以，$g^{-1}hg \in H$ 这个条件，完全等价于 $[h, g] \in H$ 这个条件。
3. 第三步 (推广到子群)：$H \unlhd G$ 的条件是“对于所有的 $g, h$”，都有 $[h, g] \in H$。这等价于说，所有形如 $[h, g]$ 的换位子构成的集合，都被包含在 $H$ 中。
4. 第四步 (生成子群)：如果所有的生成元（即所有的换位子 $[h, g]$）都在 $H$ 中，那么由它们生成的子群 $[H, G]$ 也必然被包含在 $H$ 中，即 $[H, G] \leq H$。反之，如果 $[H, G] \leq H$，那么其所有生成元 $[h, g]$ 自然也都在 $H$ 中。
   • 这就完成了 $H \unlhd G \iff [H, G] \leq H$ 的证明。

证明 (3)

这部分的证明分为三个小部分。

• 第一部分：$\sigma([x, y]) = [\sigma(x), \sigma(y)]$
• 这个证明是一个直接计算，利用了同态的性质 $\sigma(ab) = \sigma(a)\sigma(b)$ 和 $\sigma(a^{-1}) = (\sigma(a))^{-1}$。
• $\sigma([x, y]) = \sigma(x^{-1}y^{-1}xy) = \sigma(x^{-1})\sigma(y^{-1})\sigma(x)\sigma(y) = (\sigma(x))^{-1}(\sigma(y))^{-1}\sigma(x)\sigma(y) = [\sigma(x), \sigma(y)]$。

• 第二部分：$G'$ char $G$
• 原文：“因此，对于 $G^{\prime}$ 的每个换位子 $[x, y]$，$\sigma([x, y])$ 再次是一个换位子。由于 $\sigma$ 存在双边逆，因此它将换位子集合双射地映射到自身。由于换位子是 $G^{\prime}$ 的一个生成集，$\sigma\left(G^{\prime}\right)=G^{\prime}$，即 $G^{\prime}$ char $G$。”
• 解释：

1. 我们已经知道 $\sigma$ 把一个换位子 $[x,y]$ 变成另一个换位子 $[\sigma(x), \sigma(y)]$。
2. 因为 $\sigma$ 是一个自同构，它是一个双射（既是单射又是满射）。这意味着对于 $G$ 中任意一对元素 $u, v$，总能找到唯一的 $x, y$ 使得 $\sigma(x)=u, \sigma(y)=v$。所以，任何一个换位子 $[u,v]$ 都可以被表示为某个 $[x,y]$ 在 $\sigma$ 下的像。
3. 这说明 $\sigma$ 建立了“所有换位子的集合”到其自身的一个双射（bijection）。
4. $G'$ 是由这个换位子集合生成的。如果一个映射保持了生成集（将其双射到自身），那么它也必然保持由该集合生成的整个子群。即 $\sigma(G')=G'$。
5. 根据特征子群的定义，这就证明了 $G'$ 是 $G$ 的特征子群。

• 第三部分：$G/G'$ 是阿贝尔群
• 原文：“为了看出 $G / G^{\prime}$ 是Abel 群，设 $x G^{\prime}$ 和 $y G^{\prime}$ 是 $G / G^{\prime}$ 的任意元素。根据 $G / G^{\prime}$ 中群运算的定义以及 $[x, y] \in G^{\prime}$，我们有...”
• 解释：

1. 目标是证明 $(xG')(yG') = (yG')(xG')$。
2. 左边根据商群乘法定义，是 $(xy)G'$。
3. 利用命题 7(1) 的结论，$xy = yx[x,y]$。
4. 所以 $(xy)G' = (yx[x,y])G'$。
5. 根据陪集乘法法则，$(abc)H = (aH)(bH)(cH)$，这里我们可以看作 $(yx \cdot [x,y])G' = (yx)G' \cdot ([x,y])G'$。
6. 因为 $[x,y]$ 本身就是 $G'$ 的一个元素，所以陪集 $[x,y]G'$ 就是单位陪集 $G'$ 本身 (因为 $g \in H \iff gH=H$)。
7. 因此，$(yx[x,y])G' = (yx)G' \cdot G' = (yx)G'$。
8. 最后，根据商群乘法定义，$(yx)G' = (yG')(xG')$。
9. 综上，我们证明了 $(xG')(yG') = (yG')(xG')$，故 $G/G'$ 是阿贝尔群。

证明 (4)

• 第一部分：$G/H$ 阿贝尔 $\implies G' \leq H$
• 原文：“假设 $H \unlhd G$ 且 $G / H$ 是Abel 群。则对于所有 $x, y \in G$，我们有 $(x H)(y H)=(y H)(x H)$，因此...$[x, y] \in H$。”
• 解释：

1. $G/H$ 阿贝尔意味着陪集乘法可交换：$(xH)(yH) = (yH)(xH)$。
2. 即 $(xy)H = (yx)H$。
3. 两个陪集相等 $aH=bH$ 的充要条件是 $b^{-1}a \in H$。
4. 这里，$a=xy, b=yx$。所以 $(yx)^{-1}(xy) \in H$。
5. $(yx)^{-1}(xy) = x^{-1}y^{-1}xy = [x, y]$。
6. 这说明，对任意 $x, y \in G$，换位子 $[x,y]$ 都必须是 $H$ 的一个元素。
7. 既然所有换位子都在 $H$ 中，那么由它们生成的子群 $G'$ 也必然在 $H$ 中，即 $G' \leq H$。

• 第二部分：$G' \leq H \implies H \unlhd G$ 且 $G/H$ 阿贝尔
• 原文：“反之，如果 $G^{\prime} \leq H$，那么由于 (3) 中 $G / G^{\prime}$ 是**

Abel 群，所以 $G / G^{\prime}$ 的每个子群都是正规的。特别地，$H / G^{\prime} \unlhd G / G^{\prime}$。根据格同构定理，$H \unlhd G$。根据第三同构定理**...

• 解释：

1. 前提：我们假设 $G' \leq H$。$G'$ 是 $G$ 的一个子群，$H$ 是另一个包含 $G'$ 的子群。
2. 应用(3)的结论：我们已经从(3)中证明了 $G/G'$ 是一个阿贝尔群。
3. 阿贝尔群的性质：阿贝尔群有一个非常好的性质，即它的任何子群都是正规子群。
4. 格同构定理 (Lattice Isomorphism Theorem)：该定理在 $G$ 的包含 $G'$ 的子群集合与 $G/G'$ 的子群集合之间建立了一个一一对应关系。这个关系保持包含关系和正规性。
5. 推导 $H \unlhd G$：
   • 根据格同构定理，$G$ 中包含 $G'$ 的子群 $H$ 对应于商群 $G/G'$ 中的子群 $H/G'$。
   • 因为 $H/G'$ 是阿贝尔群 $G/G'$ 的一个子群，所以 $H/G'$ 必定是正规的，即 $H/G' \unlhd G/G'$。
   • 由于这个对应关系保持正规性，那么 $G$ 中对应的子群 $H$ 也必须是正规的，即 $H \unlhd G$。
6. 第三同构定理 (Third Isomorphism Theorem)：该定理指出，如果 $N \unlhd G$ 和 $H \unlhd G$ 且 $N \leq H$，那么 $G/H \cong (G/N)/(H/N)$。
7. 推导 $G/H$ 是阿贝尔群：
   • 我们让 $N = G'$。我们已经有 $G' \unlhd G$，$H \unlhd G$，以及 $G' \leq H$。所有条件都满足。
   • 应用第三同构定理，得到 $G/H \cong (G/G') / (H/G')$。
   • 我们知道 $G/G'$ 是一个阿贝尔群。一个阿贝尔群的商群仍然是阿贝尔群。（因为如果 $A$ 是阿贝尔群，$B \leq A$，那么对于商群 $A/B$ 中的任意元素 $aB, cB$，有 $(aB)(cB) = (ac)B = (ca)B = (cB)(aB)$。）
   • 因此，$(G/G')/(H/G')$ 是一个阿贝尔群。
   • Поскольку $G/H$ 同构于一个阿贝尔群，所以 $G/H$ 本身也必须是阿贝尔群。

证明 (5)

• 原文：“这是以同态的形式表述的 (4)。”
• 解释：这个证明将 (4) 的结论用同态的语言重新包装。

1. 我们有一个同态 $\varphi: G \rightarrow A$，其中 $A$ 是一个阿贝尔群。
2. 根据第一同构定理，$G/\operatorname{ker}\varphi \cong \operatorname{Im}(\varphi)$。
3. $\operatorname{Im}(\varphi)$ 是阿贝尔群 $A$ 的一个子群，所以 $\operatorname{Im}(\varphi)$ 本身也是一个阿贝尔群。
4. 因此，商群 $G/\operatorname{ker}\varphi$ 同构于一个阿贝尔群，它自身也必须是阿贝尔群。
5. 现在我们可以应用 (4) 的结论了。令 $H = \operatorname{ker}\varphi$。我们现在有 $H \unlhd G$ 并且 $G/H$ 是阿贝尔群。
6. 根据 (4) 的第一部分，这直接推导出 $G' \leq H$。
7. 将 $H = \operatorname{ker}\varphi$ 代回，我们得到 $G' \leq \operatorname{ker}\varphi$。
8. 这意味着对于 $G'$ 中的任何元素 $g'$，都有 $\varphi(g') = e_A$（$A$ 的单位元）。这正是同态分解性质的核心。交换图的存在性是同态基本定理的一个直接推论，它指出，当 $G' \leq \operatorname{ker}\varphi$ 时，就存在一个唯一的同态 $\bar{\varphi}: G/G' \to A$ 使得 $\varphi$ 可以“分解”为先进行自然投射 $\pi: G \to G/G'$，然后再应用 $\bar{\varphi}$。

本段是对前面命题7的总结，并提出了一个关于换位子子群构成的重要提醒。

第一段：

• 原文：“通过 $G$ 的换位子子群进行商，将所有换位子收缩为单位元，使得商群中的所有元素都可交换。”
• 解释：“进行商”指的是构造商群 $G/G'$。在这个商群中，原来的换位子子群 $G'$ 成为了新的单位元。任何属于 $G'$ 的元素 $g'$，其对应的陪集 $g'G'$ 就是单位陪集 $G'$。由于所有的换位子 $[x,y]$ 都在 $G'$ 中，所以它们在商群 $G/G'$ 中都“变成”了单位元。这正是导致 $G/G'$ 中元素可交换的根本原因。
• 原文：“如 (4) 所示，其强大的逆命题也成立： $G$ 对 $H$ 的商群是Abel 群当且仅当换位子子群包含在 $H$ 中...”
• 解释：这是对命题7(4)的重申和强调。它指出了 $G'$ 的“万能”特性：$G'$ 是检验一个正规子群 $H$ 能否产生阿贝尔商群的“试金石”。只要 $H$ “吞下”了 $G'$，商群 $G/H$ 就必然是阿贝尔的。

第二段：

• 原文：“我们将在下一节展示一个群（阶为 96），该群具有一个性质，即其换位子子群中的一个元素不能表示为任何 $x$ 和 $y$ 的单个换位子 $[x, y]$。因此 $G^{\prime}$ 不一定仅由（单个）换位子集合构成（而是由这些元素生成的群）。”
• 解释：这是一个非常重要的澄清，旨在纠正一个常见的误解。
• 误解：$G' = \{[x, y] \mid x, y \in G\}$，即换位子子群就是所有换位子元素的集合。
• 事实：$G' = \langle [x, y] \mid x, y \in G \rangle$，即换位子子群是由所有换位子元素生成的子群。
• 区别：生成子群的元素是生成元（这里是单个换位子）及其逆元的有限乘积。例如，$[x_1, y_1] \cdot [x_2, y_2]$ 肯定在 $G'$ 中，但它本身不一定能写成某个 $[x_3, y_3]$ 的形式。
• 例子预告：文本预告，将在第6章（原文下一节应为笔误）提供一个具体的反例：一个阶为96的群。在这个群中，存在一个元素 $z \in G'$，但你找不到任何 $x, y \in G$ 使得 $z = [x, y]$。这个 $z$ 只能通过两个或更多个换位子的乘积来得到。

本节通过四个具体的例子，展示了如何应用前面介绍的关于换位子子群的理论来确定各种群的换位子子群。

例子 (1)

• 原文：“一个群 $G$ 是Abel 群当且仅当 $G^{\prime}=1$。”
• 解释：这是换位子子群最基本的性质。
• (Abel $\Rightarrow G'=1$)：如果 $G$ 是阿贝尔群，那么对任意 $x, y \in G$，都有 $xy=yx$，这意味着 $[x, y]=x^{-1}y^{-1}xy = e$ (或 1)。$G'$ 的所有生成元都是单位元，所以 $G' = \langle 1 \rangle = \{1\}$。
• ($G'=1 \Rightarrow$ Abel)：如果 $G'=\{1\}$，那么对于任意 $x, y \in G$，它们的换位子 $[x, y]$ 必须是 $G'$ 的元素，所以 $[x, y]=1$。这意味着 $xy=yx$。这对所有元素都成立，因此 $G$ 是阿贝尔群。

例子 (2)

• 原文：“有时，我们可以在不实际显式计算换位子的情况下计算一个群的换位子子群。例如，如果 $G=D_{8}$，...”
• 解释：这个例子展示了一个非常巧妙的计算 $G'$ 的技巧，即利用命题7(4)的“夹逼”思想。
• 对 $D_8$ 的分析：

1. 寻找一个阿贝尔商群：$D_8$ 的中心 $Z(D_8)$ 是 $\{e, r^2\}$，它是一个正规子群。商群 $D_8/Z(D_8)$ 的阶是 $8/2 = 4$。任何阶为4的群都是阿贝尔群，所以 $D_8/Z(D_8)$ 是阿贝尔群。
2. 应用命题7(4) - 上界：因为 $D_8/Z(D_8)$ 是阿贝尔群，命题7(4) 告诉我们 $D_8' \leq Z(D_8)$。这给 $D_8'$ 的大小设定了一个上限。$D_8'$ 只能是 $\{e\}$ 或者 $\{e, r^2\}$。
3. 应用例子(1) - 下界：$D_8$ 不是阿贝尔群（例如 $rs \neq sr$），所以根据例子(1)，$D_8'$ 不能是平凡子群 $\{e\}$。
4. 结论：结合上界和下界，唯一的可能性就是 $D_8' = Z(D_8) = \langle r^2 \rangle$。
   • 对 $Q_8$ (四元数群) 的分析：完全相同的逻辑。$Z(Q_8) = \{\pm 1\}$。$Q_8/Z(Q_8)$ 阶为4，是阿贝尔群。所以 $Q_8' \leq Z(Q_8)$。$Q_8$ 非阿贝尔，所以 $Q_8' \neq \{1\}$。因此 $Q_8' = Z(Q_8) = \langle -1 \rangle$。
   • 推广到阶为 $p^3$ 的群：这是一个普遍结论。对于阶为 $p^3$ 的非阿贝尔群 $G$，$|Z(G)|=p$ 且 $G/Z(G)$ 是阶为 $p^2$ 的阿贝尔群。因此 $G' \leq Z(G)$。又因 $G$ 非阿贝尔，$G' \neq \{1\}$。由于 $Z(G)$ 是阶为 $p$ 的循环群，它唯一的非平凡子群就是自身。所以 $G' = Z(G)$。

例子 (3)

• 原文：“设 $D_{2 n}=\left\langle r, s \mid r^{n}=s^{2}=1, s^{-1} r s=r^{-1}\right\rangle$。...”
• 解释：这个例子再次使用“夹逼”法来确定一般二面体群 $D_{2n}$ 的换位子子群。

1. 确定下界：我们先直接计算一个具体的换位子。

$[s, r] = s^{-1}r^{-1}sr$。因为 $s^{-1}=s$，$srs=r^{-1} \implies rs=s r^{-1}$。

$[s, r] = sr^{-1}sr = (sr^{-1})sr = (rs)sr = r(s^2)r = r(e)r = r^2$。

(原文给的是 $[r,s]=r^{-2}$，我们来验证一下：$[r,s]=r^{-1}s^{-1}rs = r^{-1}s(rs) = r^{-1}s(sr^{-1}) = r^{-1}s^2r^{-1} = r^{-1}er^{-1}=r^{-2}$。两个结果生成同一个子群。)

既然 $r^2$ 是一个换位子，那么它必须在 $D_{2n}'$ 中。因此，由 $r^2$ 生成的子群 $\langle r^2 \rangle$ 也必须是 $D_{2n}'$ 的子群，即 $\langle r^2 \rangle \leq D_{2n}'$。

1. 确定上界：我们构造一个商群。考虑子群 $H = \langle r^2 \rangle$。
   • 它是正规的吗？共轭 $r$：$r(r^2)r^{-1}=r^2 \in H$。共轭 $s$：$s(r^2)s^{-1} = srsrs^{-1} = r^{-1}sr^{-1}s^{-1} = (r^{-1})^2 = r^{-2} \in H$。所以 $\langle r^2 \rangle \unlhd D_{2n}$。
   • 商群 $D_{2n}/\langle r^2 \rangle$ 是怎样的？这个商群由 $r\langle r^2 \rangle$ 和 $s\langle r^2 \rangle$ 生成。
   • $(r\langle r^2 \rangle)^2 = r^2\langle r^2 \rangle = \langle r^2 \rangle$ (单位元)，所以 $r$ 的像的阶是2。
   • $(s\langle r^2 \rangle)^2 = s^2\langle r^2 \rangle = e\langle r^2 \rangle = \langle r^2 \rangle$ (单位元)，所以 $s$ 的像的阶是2。
   • 它们可交换吗？$(s\langle r^2 \rangle)(r\langle r^2 \rangle) = sr\langle r^2 \rangle$。$(r\langle r^2 \rangle)(s\langle r^2 \rangle) = rs\langle r^2 \rangle = sr^{-1}\langle r^2 \rangle$。因为 $r^{-1} = r \cdot r^{-2}$，而 $r^{-2} \in \langle r^2 \rangle$，所以 $r^{-1}\langle r^2 \rangle = r\langle r^2 \rangle$。因此 $sr^{-1}\langle r^2 \rangle = sr\langle r^2 \rangle$。它们是可交换的。
   • 既然商群的生成元可交换，整个商群就是阿贝尔群。
   • 根据命题7(4)，这推出 $D_{2n}' \leq \langle r^2 \rangle$。
2. 结论：结合下界 $\langle r^2 \rangle \leq D_{2n}'$ 和上界 $D_{2n}' \leq \langle r^2 \rangle$，我们得到 $D_{2n}' = \langle r^2 \rangle$。
   • 关于指数的讨论：
   • $|D_{2n}'| = |\langle r^2 \rangle|$。$r$ 的阶是 $n$。$\langle r^2 \rangle$ 的阶是 $n/\text{gcd}(n,2)$。
   • 如果 $n$ 是奇数，$\text{gcd}(n,2)=1$，所以 $|\langle r^2 \rangle|=n$。此时 $\langle r^2 \rangle = \langle r \rangle$。$D_{2n}'$ 的指数是 $|D_{2n}|/|D_{2n}'| = (2n)/n = 2$。
   • 如果 $n$ 是偶数，$\text{gcd}(n,2)=2$，所以 $|\langle r^2 \rangle|=n/2$。$D_{2n}'$ 的指数是 $(2n)/(n/2) = 4$。

例子 (4)

• 原文：“由于由 $g \in G$ 进行共轭是 $G$ 的一个自同构，根据命题 (3)，... $\left[a^{g}, b^{g}\right]=[a, b]^{g}$ ...”
• 解释：
• 命题7(3)说 $\sigma([a,b]) = [\sigma(a), \sigma(b)]$。
• 共轭运算 $i_g(x) = gxg^{-1}$ 是一种自同构。将 $\sigma = i_g$ 代入，得到 $i_g([a,b]) = [i_g(a), i_g(b)]$，即 $[a,b]^g = [a^g, b^g]$。
• 重要推论：一个元素 $c$ 是换位子，当且仅当它的任何共轭 $c^g$ 也是换位子。
• 在 $S_n$ 中的应用：在 $S_n$ 中，两个置换共轭当且仅当它们有相同的循环型。所以，如果我们证明某一个特定循环型的置换（比如一个5-循环）是换位子，那么所有具有相同循环型的置换（所有5-循环）都必然是换位子。
• 对 $S_5$ 中 5-循环的分析：
• 目标是证明一个5-循环是换位子。
• 思路：找一个包含5-循环的、我们熟悉其换位子结构的子群。
• $D_{10}$：正五边形的对称群 $D_{10}$ 是 $S_5$ 的一个子群。$D_{10} = \langle r, s \rangle$，$r=(12345), s=(25)(34)$。
• 应用例子(3)：对于 $D_{10}$，$n=5$ 是奇数。所以 $D_{10}' = \langle r^2 \rangle = \langle r \rangle = \{e, r, r^2, r^3, r^4\}$。这意味着 $D_{10}$ 中所有阶为5的元素（即所有5-循环）都是 $D_{10}$ 的换位子子群中的元素。
• 问题：这只说明它们在 $D_{10}'$ 中，不代表它们是单个换位子。但原文更进一步，给出了一个具体的构造。
• 显式计算：$(14253)=[(12345),(25)(43)]$
• 设 $x=(12345), y=(25)(43)$。
• $[x, y] = x^{-1}y^{-1}xy = (15432)(25)(43)(12345)(25)(43)$。
• 我们来计算这个乘积：
• 作用于1: $1 \xrightarrow{y} 1 \xrightarrow{x} 2 \xrightarrow{y} 5 \xrightarrow{x^{-1}} 4$. 1->4.
• 作用于4: $4 \xrightarrow{y} 3 \xrightarrow{x} 4 \xrightarrow{y} 3 \xrightarrow{x^{-1}} 2$. 4->2.
• 作用于2: $2 \xrightarrow{y} 5 \xrightarrow{x} 1 \xrightarrow{y} 1 \xrightarrow{x^{-1}} 5$. 2->5.
• 作用于5: $5 \xrightarrow{y} 2 \xrightarrow{x} 3 \xrightarrow{y} 4 \xrightarrow{x^{-1}} 3$. 5->3.
• 作用于3: $3 \xrightarrow{y} 4 \xrightarrow{x} 5 \xrightarrow{y} 2 \xrightarrow{x^{-1}} 1$. 3->1.
• 结果是 $(14253)$。计算正确。
• 结论：既然特定的5-循环 $(14253)$ 是一个换位子，那么根据共轭性质，所有 $S_5$ 中的5-循环都是换位子。

本段提出了一个关于子群乘积集 $HK$ 中元素表示唯一性的重要命题。这是构建内直积理论的关键一步。

命题 8 详解

• 背景：我们考虑由两个子群 $H, K$ 的元素乘积构成的集合 $HK = \{hk \mid h \in H, k \in K\}$。注意，在一般情况下，$HK$ 不一定是一个子群。
• 核心问题：$HK$ 中的一个元素 $g$，有多少种不同的方式可以被写成 $h \in H$ 和 $k \in K$ 的乘积 $hk$？
• 结论：不同的表示方式的数量，不多不少，正好是这两个子群交集 $H \cap K$ 的阶（即元素个数）。

证明思路 (由于原文是习题，这里给出证明)

1. 假设一个元素有两种表示法：

设 $g \in HK$ 有两种表示方式：$g = h_1k_1$ 和 $g = h_2k_2$，其中 $h_1, h_2 \in H$，$k_1, k_2 \in K$。

1. 建立与交集的关系：

由 $h_1k_1 = h_2k_2$，我们可以进行代数变形：

两边左乘 $h_2^{-1}$：$h_2^{-1}h_1k_1 = k_2$

两边右乘 $k_1^{-1}$：$h_2^{-1}h_1 = k_2k_1^{-1}$

1. 分析等式两端：
   • 等式左边 $h_2^{-1}h_1$ 是两个 $H$ 中元素的乘积，所以它必然属于 $H$。
   • 等式右边 $k_2k_1^{-1}$ 是两个 $K$ 中元素的乘积，所以它必然属于 $K$。
   • 既然左右两边相等，那么这个共同的元素必须既在 $H$ 中，又在 $K$ 中。换句话说，它必须在交集 $H \cap K$ 中。
   • 我们令这个元素为 $x = h_2^{-1}h_1 = k_2k_1^{-1}$，则 $x \in H \cap K$。
2. 从交集元素反推表示法：

从 $h_2^{-1}h_1 = x$，我们得到 $h_1 = h_2x$。

从 $k_2k_1^{-1} = x$，我们得到 $k_2 = xk_1$，两边取逆元得到 $k_1 = x^{-1}k_2$。这里似乎原文推导更直接，我们换个方式：$k_2 = xk_1 \implies k_1 = x^{-1}k_2$ 是错误的。应该是 $k_2k_1^{-1} = x \implies k_2 = xk_1$。

让我们回到 $h_1k_1 = h_2k_2$ 和 $h_2^{-1}h_1 = k_2k_1^{-1} = x \in H \cap K$。

• $h_1 = h_2x$
• $k_2 = xk_1$
• 所以，任何一种其他的表示 $(h_1, k_1)$ 都可以由 $(h_2, k_2)$ 和一个交集中的元素 $x$ 得到，即 $h_1 = h_2x, k_1 = x^{-1}k_2$ (这里 $h_1k_1 = h_2x x^{-1}k_2 = h_2k_2$)。

1. 建立一一对应：
   • 给定一种表示 $g=hk$。
   • 我们可以构造出 $|H \cap K|$ 种不同的表示。对任意一个 $x \in H \cap K$，令 $h' = hx$ 且 $k' = x^{-1}k$。
   • 那么 $h' \in H$ (因为 $h, x \in H$)，$k' \in K$ (因为 $x^{-1}, k \in K$)。
   • 并且 $h'k' = (hx)(x^{-1}k) = h(xx^{-1})k = hk = g$。
   • 这种新的表示 $(h', k')$ 是不同的，除非 $x=1$。如果 $h_1=h_2x$ 且 $k_1=x^{-1}k_2$, 并且 $h_1=h_2y, k_1=y^{-1}k_2$, 那么 $h_2x = h_2y \implies x=y$。
   • 这表明，对于固定的一个表示，我们可以通过交集中的每个元素构造出一个新的、不同的表示。
   • 因此，总的表示方式数量正好是 $|H \cap K|$。

特别地 (Special Case)

• 原文：“特别地，如果 $H \cap K=1$，则 $H K$ 中的每个元素可以唯一地写成乘积 $h k$ 的形式...”
• 解释：这是上述结论的直接推论。如果交集只有一个元素（单位元），即 $|H \cap K|=1$，那么表示方式的数量就是 1。这意味着对 $HK$ 中的任何元素 $g$，都只存在唯一的一对 $(h, k)$ ($h \in H, k \in K$) 使得 $g = hk$。

这是本节的核心定理，给出了判断一个群的子群乘积何时同构于外直积的充分条件。

定理 9 详解

• 前提条件：定理要求两个子群 $H$ 和 $K$ 必须同时满足两个条件：

1. 都是正规子群：$H \unlhd G$ 并且 $K \unlhd G$。这是一个非常强的条件。不仅仅是其中一个正规，而是两者都正规。
2. 交集平凡：$H \cap K = \{1\}$。它们除了单位元之外没有公共元素。

• 结论：如果这两个条件满足，那么由它们构成的子群乘积 $HK$ 在结构上就等同于 (同构于) 外直积 $H \times K$。

定理证明的逻辑链条 (原文在下一段，这里先概述)

1. 证明 $HK$ 是一个子群：由于 $H$ (或 $K$) 是正规的，可以保证 $HK=KH$，所以 $HK$ 是 $G$ 的一个子群。
2. 证明 $H$ 和 $K$ 的元素可交换：对于任意 $h \in H, k \in K$，证明 $hk=kh$。这是利用两个子群都是正规子群这一关键条件得出的。
3. 构建映射：定义一个从 $HK$ 到 $H \times K$ 的映射 $\varphi$。
4. 证明映射是良定义的：利用命题8的结论，因为 $H \cap K = \{1\}$，所以 $HK$ 中每个元素 $g$ 都能唯一地写成 $hk$ 的形式。因此，$\varphi(hk) = (h, k)$ 是没有歧义的，是良定义的。
5. 证明映射是同态：证明 $\varphi(g_1g_2) = \varphi(g_1)\varphi(g_2)$。这里会用到第2步证明的 $h, k$ 元素的可交换性。
6. 证明映射是双射：证明 $\varphi$ 既是单射也是满射。这同样源于表示的唯一性和 $HK$ 的构造本身。
7. 结论：一个良定义的、双射的同态就是一个同构。因此 $HK \cong H \times K$。

本段详细阐述了定理9的证明过程，分为三个主要步骤。

第一步：证明 $H$ 和 $K$ 的元素逐点可交换

• 原文：“...设 $h \in H$ 且 $k \in K$。由于 $H \unlhd G$， $k^{-1} h k \in H$，因此 $h^{-1}\left(k^{-1} h k\right) \in H$。类似地，$\left(h^{-1} k^{-1} h\right) k \in K$。由于 $H \cap K=1$，因此 $h^{-1} k^{-1} h k=1$，即 $h k=k h$...”
• 解释：这是证明中最巧妙的部分。目标是证明对任意 $h \in H, k \in K$, 都有 $hk=kh$，这等价于证明它们的换位子 $[h,k] = h^{-1}k^{-1}hk$ 等于单位元 1。
• 考虑换位子 $c = h^{-1}k^{-1}hk$。
• 从 $H$ 的角度看：
• 因为 $H \unlhd G$（$H$是正规子群），所以对于任何 $k \in G$ (这里 $k \in K \subset G$) 和 $h \in H$，有 $k^{-1}hk \in H$。
• 既然 $k^{-1}hk \in H$，而 $h^{-1}$ 也显然在 $H$ 中，那么它们的乘积 $h^{-1}(k^{-1}hk)$ 必须在 $H$ 中（因为 $H$ 是子群，对乘法封闭）。
• 所以， $c \in H$。
• 从 $K$ 的角度看：
• 因为 $K \unlhd G$（$K$也是正规子群），所以对于任何 $h \in G$ (这里 $h \in H \subset G$) 和 $k \in K$，有 $h^{-1}kh \in K$。
• 换位子 $c = h^{-1}k^{-1}hk$ 可以重新组合成 $(h^{-1}k^{-1}h)k$。
• 既然 $k \in K$，而 $h^{-1}k^{-1}h$ 是 $k^{-1} \in K$ 的共轭，由于 $K$ 正规，所以 $h^{-1}k^{-1}h \in K$。
• 那么它们的乘积 $(h^{-1}k^{-1}h)k$ 必须在 $K$ 中。
• 所以， $c \in K$。
• 结合交集条件：
• 我们证明了同一个元素 $c$ 既属于 $H$ 又属于 $K$。
• 因此，$c$ 必须属于它们的交集 $H \cap K$。
• 根据定理的条件 (2)，$H \cap K = \{1\}$。
• 所以 $c$ 只能是单位元，即 $h^{-1}k^{-1}hk = 1$。
• 两边左乘 $kh$，得到 $kh(h^{-1}k^{-1}hk) = kh \cdot 1$，即 $hk=kh$。
• 结论：在定理的条件下，来自 $H$ 的任意元素和来自 $K$ 的任意元素都可交换。

第二步：构建映射并证明其为同态

• 良定义性 (Well-definedness)
• 原文：“根据前面的命题，$H K$ 中的每个元素可以唯一地写成乘积 $h k$ 的形式... 因此映射...是良定义的。”
• 解释：我们想定义映射 $\varphi(g) = (h,k)$，其中 $g=hk$。要使这个映射成立，必须保证对于每个输入 $g$，只有一个输出 $(h,k)$。命题8已经告诉我们，表示的唯一性恰好由条件 $H \cap K=\{1\}$ 保证。因此，这个映射的定义没有歧义。
• 证明同态 (Homomorphism)
• 原文：“为了看出 $\varphi$ 是一个同态... $\left(h_{1} k_{1}\right)\left(h_{2} k_{2}\right)=\left(h_{1} h_{2}\right)\left(k_{1} k_{2}\right)$ ...”
• 解释：我们需要证明 $\varphi(g_1 g_2) = \varphi(g_1) \varphi(g_2)$。
• 设 $g_1 = h_1k_1$ 和 $g_2 = h_2k_2$ 是 $HK$ 中的任意两个元素。
• 它们的乘积是 $g_1g_2 = (h_1k_1)(h_2k_2)$。
• 关键步骤：利用刚刚证明的交换性。因为 $k_1 \in K$ 且 $h_2 \in H$，所以 $k_1h_2 = h_2k_1$。
• $g_1g_2 = h_1(k_1h_2)k_2 = h_1(h_2k_1)k_2 = (h_1h_2)(k_1k_2)$。
• 这个结果 $(h_1h_2)(k_1k_2)$ 的形式是一个 $H$ 中的元素 ($h_1h_2$) 乘以一个 $K$ 中的元素 ($k_1k_2$)。这正是 $\varphi$ 定义所需要的 $hk$ 形式。
• 应用 $\varphi$：
• $\varphi(g_1g_2) = \varphi((h_1h_2)(k_1k_2)) = (h_1h_2, k_1k_2)$ (根据 $\varphi$ 的定义)。
• 另外，$\varphi(g_1) = (h_1, k_1)$ 和 $\varphi(g_2) = (h_2, k_2)$。
• 在外直积 $H \times K$ 中，乘法是按分量定义的：$\varphi(g_1)\varphi(g_2) = (h_1, k_1)(h_2, k_2) = (h_1h_2, k_1k_2)$。
• 比较两边的结果，我们发现 $\varphi(g_1g_2) = \varphi(g_1)\varphi(g_2)$。因此 $\varphi$ 是一个同态。

第三步：证明映射为双射 (Bijection)

• 原文：“同态 $\varphi$ 是一个双射，因为 $H K$ 的每个元素表示为 $h k$ 形式的乘积是唯一的，这就证明了 $\varphi$ 是一个同构。”
• 解释：
• 单射 (Injective)：如果 $\varphi(g_1) = \varphi(g_2)$，是否能推出 $g_1=g_2$？
• 设 $g_1=h_1k_1, g_2=h_2k_2$。$\varphi(g_1)=(h_1,k_1), \varphi(g_2)=(h_2,k_2)$。
• 如果 $(h_1,k_1) = (h_2,k_2)$，那么根据有序对相等的定义，必须有 $h_1=h_2$ 且 $k_1=k_2$。
• 这直接导致 $g_1=h_1k_1=h_2k_2=g_2$。所以 $\varphi$ 是单射。
• （另一种方式：$\ker\varphi = \{g=hk \in HK \mid \varphi(g)=(1,1)\}$。这意味着 $h=1, k=1$，所以 $g=1\cdot1=1$。核是平凡的，所以映射是单射。）
• 满射 (Surjective)：对于 $H \times K$ 中任意一个元素 $(h, k)$，是否存在 $g \in HK$ 使得 $\varphi(g)=(h,k)$？
• 当然存在。我们只需取 $g = hk$。这个 $g$ 就在 $HK$ 的定义域中。
• 根据 $\varphi$ 的定义，$\varphi(g) = \varphi(hk) = (h,k)$。
• 所以 $\varphi$ 是满射。
• 结论：$\varphi$ 是一个良定义的、双射的同态，因此它是一个同构 (isomorphism)。证明完毕。

本段基于定理9的结论，正式定义了“内直积”和“外直积”，并阐明了它们之间的关系。

定义部分

• 内直积 (Internal Direct Product)：
• 条件：在一个群 $G$ 内部，找到了两个子群 $H$ 和 $K$，它们满足：

1. $H \unlhd G$ (H是正规子群)
2. $K \unlhd G$ (K是正规子群)
3. $H \cap K = \{1\}$ (交集平凡)
   • 定义：满足这些条件的子群乘积 $HK$ 被称为 $H$ 和 $K$ 的内直积。
   • 外直积 (External Direct Product)：
   • 回顾：这是我们之前学习的概念。给定任意两个群 $H$ 和 $K$（它们可以毫不相关），我们构建一个新的群，其元素是所有可能的有序对 $(h, k)$，运算是按分量进行的。这个构造出来的群 $H \times K$ 称为外直积。

两者关系

• 原文：“内直积和外直积之间的区别...纯粹是记号上的...”
• 解释：定理9告诉我们，只要条件满足，内直积 $HK$ 就和外直积 $H \times K$ 是同构的。这意味着从抽象代数的角度看，它们的“群结构”是完全一样的。
• 区别体现在记号上：
• 内直积的元素是 $G$ 中的元素，我们习惯将它们写成乘积形式 $hk$。它们生活在“大”群 $G$ 内部。
• 外直积的元素是我们构造出来的有序对 $(h, k)$。它们生活在一个新的、独立的空间中。
• 同构映射 $\varphi: hk \mapsto (h, k)$ 就是连接这两种记号的桥梁。

例子说明

• 原文：“例如，当 $Z_{n}=\langle a\rangle$ 和 $Z_{m}=\langle b\rangle$ 时，我们写 $x=(a, 1)$ 和 $y=(1, b)$，因此 $Z_{n} \times Z_{m}$ 的每个元素都写成 $x^{r} y^{s}$ 的形式。”
• 解释：这个例子说明了我们实际上经常在不自觉地模糊这两种记号。
• 考虑外直积 $G = Z_n \times Z_m$。
• 我们可以识别出它内部的两个子群：
• $H = \{(a^r, 1) \mid r \in Z\} \cong Z_n$
• $K = \{(1, b^s) \mid s \in Z\} \cong Z_m$
• 在 $G$ 中，$H$ 和 $K$ 满足定理9的条件（因为 $G$ 阿贝尔，所以它们都正规，且交集显然是 $\{(1,1)\}$）。
• 因此 $G = HK$，是 $H$ 和 $K$ 的内直积。
• $G$ 中的任何一个元素 $(a^r, b^s)$，可以看作是外直积的有序对，也可以看作是内直积中两个元素的乘积：$(a^r, 1) \cdot (1, b^s)$。
• 如果我们用 $x$ 代表生成元 $(a,1)$，用 $y$ 代表生成元 $(1,b)$，那么任何元素都可以写成 $x^r y^s$。这种写法看起来就像内直积的 $hk$ 形式，尽管我们最初是从外直积出发的。

本节通过三个具体的、更复杂的例子，展示了如何应用定理9来分解群的结构。

例子 (1): 分解二面体群

• 目标：证明当 $n$ 是奇数时，$D_{4n} \cong D_{2n} \times Z_2$。
• 策略：在 $D_{4n}$ 内部找到两个子群 $H$ 和 $K$，验证它们满足定理9的条件，并证明 $D_{4n}=HK$。
• 构造子群：
• $D_{4n} = \langle r, s \mid r^{2n}=1, s^2=1, srs=r^{-1} \rangle$。
• $H = \langle s, r^2 \rangle$。
• $K = \langle r^n \rangle$。
• 验证条件：

1. $H \unlhd D_{4n}$?
   • $H$ 是由 $s$ 和 $r^2$ 生成的。$|H|$ 是多少？$H$ 的元素是形如 $(r^2)^i s^j$。可以证明 $H$ 的阶是 $2n$。
   • $|D_{4n}| = 4n$。所以 $H$ 在 $D_{4n}$ 中的指数是 $4n / (2n) = 2$。
   • 任何指数为2的子群都是正规子群。所以 $H \unlhd D_{4n}$。
2. $K \unlhd D_{4n}$?
   • $K = \langle r^n \rangle = \{e, r^n\}$，因为 $(r^n)^2 = r^{2n} = e$。
   • 我们需要证明 $K$ 在 $D_{4n}$ 的中心 $Z(D_{4n})$ 里。
   • $r$ 和 $r^n$ 显然可交换，因为它们都是 $r$ 的幂。
   • $s$ 和 $r^n$ 可交换吗？$sr^ns^{-1} = (srs^{-1})^n = (r^{-1})^n = r^{-n}$。
   • 我们需要 $r^{-n} = r^n$，即 $r^{2n}=e$。这个条件是满足的。所以 $sr^ns^{-1}=r^n$。
   • 等一下，这里原文的推导 $s r^n s = r^{-n} = r^n$ 是有问题的。$r^{-n}=r^n$ 仅当 $r^{2n}=e$ 且 $r^n$ 的阶是2时成立，即 $r^{2n}=e$。不对，应该是 $r^{2n}=e$ 和 $r^n \ne e$ 蕴含 $r^n = r^{-n}$ 吗？不，是 $(r^n)^2=e$ 蕴含 $r^n=(r^n)^{-1}=r^{-n}$。这在 $r$ 的阶为 $2n$ 时成立。所以 $sr^n s^{-1} = r^{-n} = (r^n)^{-1}$。这里原文的 $s r^n s = r^{-n} = r^n$ 是在 $s$ 与 $r^n$ 可交换的条件下才成立的。
   • 让我们重新检查 $s$ 与 $r^n$ 的交换性：$s r^n s^{-1} = (r^{-1})^n = r^{-n}$。我们需要 $r^{-n}=r^n$，这意味着 $r^{2n}=e$。这是 $D_{4n}$ 定义的一部分。所以 $s$ 与 $r^n$ 并不交换，而是 $s r^n s^{-1} = r^{-n}$。
   • 但是，当 $n$ 是奇数时，$r^{-n} = r^{2n} \cdot r^{-n} = r^n$。这个等式成立！$r^{2n}=e$, 所以 $r^n = r^{-n}$。
   • 更正：$srs = r^{-1}$，所以 $sr^ns = (srs)^n = (r^{-1})^n = r^{-n}$。我们需要 $sr^n = r^ns$。即 $sr^n = sr^{-n}$，所以 $r^n=r^{-n}$，即 $r^{2n}=e$。这个条件始终成立。所以 $s$ 和 $r^n$ 始终交换！
   • 重新思考：$s r^n s = r^{-n}$。$r^n$ 要在中心里，需要 $r^n$ 与 $s$ 交换，即 $sr^ns = r^n$。所以需要 $r^{-n}=r^n$，这等价于 $(r^n)^2=e$，即 $r^{2n}=e$。这是对的。所以 $K = \langle r^n \rangle$ 始终在 $D_{4n}$ 的中心里。
   • 既然 $K \leq Z(D_{4n})$，那么 $K$ 肯定是正规子群。$K \unlhd D_{4n}$。
3. $H \cap K = \{e\}$?
   • $H=\langle s, r^2 \rangle$。$K=\langle r^n \rangle = \{e, r^n\}$。
   • 交集不为 $\{e\}$ 的唯一可能是 $r^n \in H$。
   • $H$ 中的旋转元素都是 $r^2$ 的幂，即 $r^{2k}$。
   • 如果 $r^n \in H$，那么 $r^n$ 必须能表示为 $r^{2k}$ 的形式。
   • 这意味着 $n$ 必须是偶数。
   • 但定理的前提是 $n$ 是奇数。当 $n$ 是奇数时，$r^n$ 不可能是 $r$ 的偶数次幂。
   • 因此，$r^n \notin H$。所以 $H \cap K = \{e\}$。
   • 应用定理9
   • 所有条件都满足了。所以 $HK \cong H \times K$。
   • $H = \langle s, r^2 \rangle$。令 $r_1=r^2, s_1=s$。$r_1^n = (r^2)^n = r^{2n}=e$, $s_1^2=s^2=e$, $s_1r_1s_1^{-1}=sr^2s^{-1}=(srs^{-1})^2=(r^{-1})^2=r^{-2}=(r^2)^{-1}=r_1^{-1}$。所以 $H$ 的表示是 $\langle r_1, s_1 \mid r_1^n=s_1^2=1, s_1r_1s_1^{-1}=r_1^{-1} \rangle$，这正是 $D_{2n}$ 的定义。所以 $H \cong D_{2n}$。
   • $K=\langle r^n \rangle$ 是阶为2的循环群，所以 $K \cong Z_2$。
   • $|HK| = |H||K|/|H \cap K| = (2n)(2)/1 = 4n$。
   • $|D_{4n}| = 4n$。
   • 因为 $HK$ 是 $D_{4n}$ 的子群且阶数相同，所以 $D_{4n} = HK$。
   • 最终结论：$D_{4n} = HK \cong H \times K \cong D_{2n} \times Z_2$。

例子 (2): 分解集合稳定子

• 目标：证明 $S_n$ 中一个子集 $I$ 的集合稳定子 $G$ 同构于 $S_I \times S_J$。
• 定义：
• $I \subseteq \{1, \dots, n\}$，$J$ 是其补集。$|I|=n-m, |J|=m$。
• $G = \{\sigma \in S_n \mid \sigma(I)=I\}$。这意味着 $\sigma$ 把 $I$ 中的元素映射到 $I$ 中，把 $J$ 中的元素映射到 $J$ 中。
• $H = \{\sigma \in G \mid \sigma(i)=i \text{ for all } i \in I\}$。$H$ 是 $G$ 中逐点固定 $I$ 的置换集合。
• $K = \{\tau \in G \mid \tau(j)=j \text{ for all } j \in J\}$。$K$ 是 $G$ 中逐点固定 $J$ 的置换集合。
• 验证条件：

1. $H, K$ 正规吗？
   • $H$ 是 $G$ 在 $I$ 上的作用的核，核总是正规子群。或者直接验证：对任意 $g \in G, h \in H$，要证明 $g h g^{-1} \in H$。即证明 $ghg^{-1}$ 逐点固定 $I$。对任意 $i \in I$, 设 $i' = g(i) \in I$。则 $g^{-1}(i')=i$。$ghg^{-1}(i') = gh(i) = g(i) = i'$。不对，这个推导是错的。
   • 让我们重新来：设 $i \in I$。我们要看 $ghg^{-1}(i)$ 是什么。因为 $g \in G$ (集合稳定子)，$g^{-1}(i)$ 不一定等于 $i$，但它一定在 $I$ 中。设 $i' = g^{-1}(i) \in I$。因为 $h \in H$ (逐点固定 $I$)，所以 $h(i')=i'$。那么 $ghg^{-1}(i) = gh(i') = g(i') = g(g^{-1}(i)) = i$。所以 $ghg^{-1}$ 确实逐点固定了 $I$ 的所有元素。因此 $ghg^{-1} \in H$。所以 $H \unlhd G$。
   • 同理可证 $K \unlhd G$。
2. $H \cap K = \{e\}$?
   • 如果一个置换 $\sigma \in H \cap K$，那么它既要逐点固定 $I$ 的所有元素，也要逐点固定 $J$ 的所有元素。
   • $I \cup J = \{1, \dots, n\}$。所以 $\sigma$ 必须固定所有 $n$ 个元素。
   • 唯一能做到这点的置换就是单位元 $e$。所以 $H \cap K = \{e\}$。
3. $G=HK$?
   • 任何一个 $\sigma \in G$，它保持 $I$ 和 $J$ 不变。这意味着 $\sigma$ 的循环分解中，每个循环要么只包含 $I$ 的元素，要么只包含 $J$ 的元素。不会有循环跨越 $I, J$。
   • 我们可以把 $\sigma$ 分解成两部分：$\sigma_J$ 是 $\sigma$ 在 $J$ 上的作用部分（在 $I$ 上是恒等），$\sigma_I$ 是 $\sigma$ 在 $I$ 上的作用部分（在 $J$ 上是恒等）。
   • $\sigma_J$ 只动 $J$ 的元素，所以它逐点固定 $I$。因此 $\sigma_J \in H$。
   • $\sigma_I$ 只动 $I$ 的元素，所以它逐点固定 $J$。因此 $\sigma_I \in K$。
   • 并且 $\sigma = \sigma_J \sigma_I$ (因为它们作用在不相交的集合上，所以可交换)。
   • 因此 $G=HK$。
   • 应用定理9
   • $G = HK \cong H \times K$。
   • $H$ 中的置换只动 $J$ 上的点，实际上就是 $J$ 上的所有置换的集合。所以 $H \cong S_J \cong S_m$。
   • $K$ 中的置换只动 $I$ 上的点，实际上就是 $I$ 上的所有置换的集合。所以 $K \cong S_I \cong S_{n-m}$。
   • 最终结论：$G \cong S_m \times S_{n-m}$。

例子 (3): 分解中心化子

• 目标：确定 $S_n$ 中一个置换 $\sigma$ 的中心化子 $C_{S_n}(\sigma)$ 的结构。
• 定义：
• $\sigma \in S_n$。
• $I = \{i \mid \sigma(i)=i\}$，被 $\sigma$ 固定的点的集合。$J$ 是补集，即 $\sigma$ 移动的点的集合。
• $C=C_{S_n}(\sigma) = \{\tau \in S_n \mid \tau\sigma = \sigma\tau\}$。
• 分析：

1. $C$ 稳定 $I, J$：如果 $i \in I$, $\tau \in C$, 则 $\sigma(\tau(i)) = \tau(\sigma(i)) = \tau(i)$。这意味着 $\tau(i)$ 也是被 $\sigma$ 固定的点，所以 $\tau(i) \in I$。因此 $C$ 是 $I$ (和 $J$) 的集合稳定子。
2. 应用例子(2)的框架：既然 $C$ 是一个集合稳定子，它本身具有一个直积结构。$C \le S_I \times S_J$ (这里 $S_I$ 指作用在 $I$ 上的对称群， $S_J$ 指作用在 $J$ 上的对称群)。
   • 任何 $\alpha \in C$ 都可以唯一分解为 $\alpha = \alpha_I \alpha_J$，其中 $\alpha_I$ 只动 $I$ 的点，$\alpha_J$ 只动 $J$ 的点。
3. 确定 $C$ 的具体形式：$\alpha = \alpha_I \alpha_J$ 要在 $C$ 中，必须满足 $\alpha\sigma = \sigma\alpha$。
   • $(\alpha_I \alpha_J)\sigma = \sigma(\alpha_I \alpha_J)$
   • $\sigma$ 只在 $J$ 上有非平凡作用，所以它与在 $I$ 上作用的 $\alpha_I$ 可交换：$\sigma\alpha_I = \alpha_I\sigma$。
   • 代入上式：$\alpha_I \alpha_J \sigma = \alpha_I \sigma \alpha_J$。消去 $\alpha_I$ 得 $\alpha_J \sigma = \sigma \alpha_J$。
   • 所以，$\alpha$ 在中心化子中 $\iff \alpha_J$ 与 $\sigma$ 可交换。
4. $\alpha_I$ 的限制：对 $\alpha_I$ 没有任何限制。它可以是任何作用在 $I$ 上的置换。所以 $\alpha_I$ 来自于整个 $S_I$。这部分构成了 $K \cong S_I$。
5. $\alpha_J$ 的限制：$\alpha_J$ 是一个作用在 $J$ 上的置换，且必须与 $\sigma$ (限制在 $J$ 上的部分) 可交换。这正是 $\sigma$ 在群 $S_J$ 中的中心化子 $C_{S_J}(\sigma)$。这部分构成了 $H \cong C_{S_J}(\sigma)$。
   • 结论：$C_{S_n}(\sigma) \cong C_{S_J}(\sigma) \times S_I$。
   • 特殊情况：m-循环：
   • 如果 $\sigma$ 是一个 $m$-循环，那么 $J$ 是它移动的 $m$ 个点，$I$ 是它不动的 $n-m$ 个点。
   • 在 $S_J$ (阶为 $m!$ 的对称群) 中，一个 $m$-循环的中心化子就是它自身生成的循环群，阶为 $m$。即 $C_{S_J}(\sigma) = \langle \sigma \rangle$。
   • $S_I$ 就是作用在 $n-m$ 个点上的对称群 $S_{n-m}$。
   • 最终结论：$C_{S_n}(\sigma) \cong \langle \sigma \rangle \times S_{n-m}$。
   • 阶数验证：这个群的阶是 $m \times (n-m)!$，这与我们之前用轨道-稳定化子定理计算出的中心化子阶数结果一致。

这部分是本章的习题，旨在巩固本节所学的概念，包括换位子、换位子子群、内直积识别定理及其应用。以下对部分习题的思路进行解析：

1. 思路:
   • $[y, x] = y^{-1}x^{-1}yx$。计算 $[x, y]^{-1} = (x^{-1}y^{-1}xy)^{-1} = y^{-1}x^{-1}(y^{-1})^{-1}(x^{-1})^{-1} = y^{-1}x^{-1}yx$。两者相等。
   • $[A, B] = \langle [a,b] \mid a \in A, b \in B \rangle$。$[B, A] = \langle [b,a] \mid b \in B, a \in A \rangle$。
   • 由于 $[b,a] = [a,b]^{-1}$，一个子群的生成集中的所有元素的逆元，生成的子群是同一个子群。即 $\langle S \rangle = \langle S^{-1} \rangle$。因此 $[A,B]=[B,A]$。
2. 思路: 这是命题7(2)的证明，原文中已给出。要求自己独立证明一遍。
3. 思路: 这是换位子的恒等式，需要直接展开定义进行代数运算。
   • (a) $[a, c](c^{-1}[a, b] c) = (a^{-1}c^{-1}ac)(c^{-1}(a^{-1}b^{-1}ab)c) = a^{-1}c^{-1}a(c c^{-1})a^{-1}b^{-1}ab c = a^{-1}c^{-1}b^{-1}abc = a^{-1}(bc)^{-1}a(bc) = [a, bc]$。
   • (b) 类似地展开即可。
4. 思路:
   • $S_4/A_4 \cong Z_2$，是阿贝尔群。所以 $S_4' \le A_4$。
   • $A_4$ 的商群 $A_4/V_4 \cong Z_3$，是阿贝尔群 ($V_4$ 是克莱因四元群)。所以 $A_4' \le V_4$。
   • $A_4$ 非阿贝尔（例如 $(123)(124) \neq (124)(123)$），所以 $A_4' \neq \{e\}$。
   • 计算 $A_4$ 中一个换位子，如 $[(123), (124)] = (132)(142)(123)(124) = (12)(34) \in V_4$。
   • 可以证明 $V_4$ 中所有非单位元元素都可以表示成换位子，且 $A_4'$ 不可能比 $V_4$ 更小。所以 $A_4' = V_4$。
   • 由于 $S_4' \le A_4$，且 $S_4$ 非阿贝尔，所以 $S_4'$ 是非平凡的。$S_4/V_4$ 的阶是 $24/4=6$，同构于 $S_3$，非阿贝尔。所以 $S_4'$ 不可能 $\le V_4$。这说明 $S_4' = A_4$。
5. 思路:
   • $A_n$ 在 $n \ge 5$ 时是单群。
   • $S_n' \unlhd S_n$。我们知道 $S_n' \le A_n$。
   • 因为 $S_n$ 非阿贝尔， $S_n' \neq \{e\}$。
   • $A_n$ 是单群，它内部只有 $\{e\}$ 和 $A_n$ 两个正规子群。$S_n'$ 作为 $S_n$ 的正规子群，不一定是 $A_n$ 的正规子群。
   • 但是 $S_n'$ 是特征子群，所以它在 $S_n$ 的任何自同构下不变，也就一定是正规子群。
   • $A_n$ 也是 $S_n$ 的正规子群。$[S_n', A_n] \le S_n' \cap A_n = S_n'$。
   • 正确的思路是：$S_n/A_n \cong Z_2$ 是阿贝尔群，所以 $S_n' \leq A_n$。又因为 $A_n$ 是非阿贝尔单群，它的换位子子群 $A_n'$ 是 $A_n$ 的一个正规子群，且 $A_n$ 非阿贝尔所以 $A_n' \neq \{e\}$。因为 $A_n$ 是单群，所以 $A_n'=A_n$。$A_n \le S_n'$？是的。所有3-循环都在 $A_n$ 中，可以证明所有3-循环都是 $S_n$ 中的换位子。因此 $A_n = \langle \text{3-cycles} \rangle \le S_n'$。结合 $S_n' \le A_n$，得到 $S_n' = A_n$。
6. 思路: 设 $G$ 是有限阿贝尔群。设其 Sylow p-子群为 $P_1, P_2, \dots, P_k$。
   • 因为 $G$ 阿贝尔，所有子群都是正规的。所以 $P_i \unlhd G$ for all $i$。
   • 根据拉格朗日定理，$P_i \cap P_j = \{e\}$ for $i \neq j$ (因为它们的阶互素)。
   • 应用定理9的推广（对多个子群），$P_1P_2\dots P_k \cong P_1 \times P_2 \times \dots \times P_k$。
   • 这个乘积子群的阶是 $|P_1||P_2|\dots|P_k| = |G|$。
   • 所以 $G = P_1P_2\dots P_k \cong P_1 \times P_2 \times \dots \times P_k$。
7. 思路: 这是一个陷阱题。例子(1)证明了当 $n$ 是奇数时，$D_{4n} \cong D_{2n} \times Z_2$。题目要求证明 $D_{8n}$ (原文 $D_{8n}$ 应该是笔误，可能指 $n$ 是偶数的情况，比如 $D_{4 \times (2k)}$) 与 $D_{4n} \times Z_2$ 不同构。
   • 考虑 $n=2$，我们要比较 $D_{16}$ 和 $D_8 \times Z_2$。
   • 比较它们的中心。$Z(D_{16}) = \langle r^8 \rangle$，阶为2。
   • $Z(D_8 \times Z_2) = Z(D_8) \times Z(Z_2) = \langle r^4 \rangle_{D_8} \times Z_2$。这是一个阶为 $2 \times 2=4$ 的群 ($V_4$)。
   • 由于中心不同构，原群也不同构。
8. 思路:
   • $G/A$ 阿贝尔 $\implies G' \le A$。
   • $G/B$ 阿贝尔 $\implies G' \le B$。
   • 所以 $G'$ 被包含在 $A$ 和 $B$ 的交集中，$G' \le A \cap B$。
   • 令 $H = A \cap B$。因为 $G' \le H$，根据命题7(4)的逆命题， $G/H = G/(A \cap B)$ 是阿贝尔群。